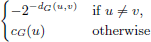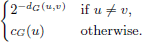Spectra of closeness Laplacian and closeness signless Laplacian of graphs

School of Mathematical Sciences, South China Normal University, Guangzhou 510631, P.R. China

^* Corresponding author: zhoubo@scnu.edu.cn

Received: 6 August 2022
Accepted: 14 September 2022

Abstract

For a graph G with vertex set V(G) and u, v ∈ V(G), the distance between vertices u and v in G, denoted by d_G(u,v), is the length of a shortest path connecting them and it is ∞ if there is no such a path, and the closeness of vertex u in G is c_G(u) = ∑_w∈V(G)^2-d_G^(u,w). Given a graph G that is not necessarily connected, for u, v∈V(G), the closeness matrix of G is the matrix whose (u,v)-entry is equal to 2^-d_G^(u,v) if u≠v and 0 otherwise, the closeness Laplacian is the matrix whose (u,v)-entry is equal to

$$\{\begin{array}{c}-2^{-d_G(u,v)}\hspace{1em}\mathrm{if} u\ne v, \\ c_G\left(u\right)\hspace{1em}\hspace{1em}\mathrm{otherwise}\hspace{0.5em}\end{array}\hspace{0.5em}$$

and the closeness signless Laplacian is the matrix whose (u,v)-entry is equal to

$$\{\begin{array}{c}{2}^{-d_G(u,v)}\hspace{1em}\hspace{1em}\&\mathrm{if} \mathrm{u}\ne \mathrm{v},\\ c_G\left(u\right)\hspace{1em}\hspace{1em}\mathrm{otherwise}.\end{array}$$

We establish relations connecting the spectral properties of closeness Laplacian and closeness signless Laplacian and the structural properties of graphs. We give tight upper bounds for all nontrivial closeness Laplacian eigenvalues and characterize the extremal graphs, and determine all trees and unicyclic graphs that maximize the second smallest closeness Laplacian eigenvalue. Also, we give tight upper bounds for the closeness signless Laplacian eigenvalues and determine the trees whose largest closeness signless Laplacian eigenvalues achieve the first two largest values.