EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 56 / No 2 (March-April 2022) RAIRO-Oper. Res., 56 2 (2022) 979-1012 References
Open Access
Issue
RAIRO-Oper. Res.
Volume 56, Number 2, March-April 2022
Page(s) 979 - 1012
DOI https://doi.org/10.1051/ro/2021167
Published online 14 April 2022
  • K. Abbas and D. Aissani, Approximation of performance measures in an M/G/1 queue with breakdowns. Qual. Technol. Quant. Manage. 7 (2010) 353–363. [Google Scholar]
  • M. Agiwal, A. Roy and N. Saxena, Next generation 5G wireless networks: a comprehensive survey. IEEE Commun. Surv. Tutorials 18 (2016) 1617–1655. [CrossRef] [Google Scholar]
  • M. Baruah, K.C. Madan and T. Eldabi, Balking and re-service in a vacation queue with arrival and two types of heterogeneous service. J. Math. Res. 4 (2012) 1114–1124. [Google Scholar]
  • A. Begum and G. Choudhury, Analysis of an unreliable single server batch arrival queue with two types of services under Bernoulli vacation policy. Commun. Stat. Theory Methods 50 (2021) 2136–2160. [CrossRef] [Google Scholar]
  • G. Choudhury and M. Deka, A single server queueing system with two phases of service subject to server breakdown and Bernoulli vacation. Appl. Math. Modell. 36 (2012) 6050–6060. [Google Scholar]
  • G. Choudhury and M. Deka, A batch arrival unreliable server delaying repair queue with two phases of service and Bernoulli vacation under multiple vacation policy. Qual. Technol. Quant. Manage. 15 (2018) 157–186. [Google Scholar]
  • G. Choudhury and C.R. Kalita, An M/G/1 queue with two types of general heterogeneous service and optional repeated service subject to server’s breakdown and delayed repair. Qual. Technol. Quant. Manage. 15 (2017) 622–654. [Google Scholar]
  • G. Choudhury and M. Paul, A batch arrival queue with a second optional service channel under N-policy. Stoch. Anal. App. 24 (2006) 1–21. [Google Scholar]
  • G. Choudhury, J.C. Ke and L. Tadj, The N-policy for an unreliable server with delaying repair and two phases of service. J. Comput. Appl. Math. 231 (2009) 349–364. [Google Scholar]
  • D.R. Cox, The analysis of non-Markovian stochastic processes by the inclusion of supplementary variables. Math. Proc. Cambridge Philos. Soc. 51 (1955) 433–441. [Google Scholar]
  • I. Dimitriou, A modified vacation queueing model and its application on the Discontinuous Reception power saving mechanism in unreliable Long Term Evolution networks. Perform Eval. 77 (2014) 37–56. [Google Scholar]
  • B.T. Doshi, Queueing systems with vacations a survey. Queueing Syst. 1 (1986) 29–66. [Google Scholar]
  • S.A. Fowler, A. Mellouk and N. Yamada, LTE-Advanced DRX Mechanism for Power Saving. Wiley, New York (2013). [CrossRef] [Google Scholar]
  • A. Gautam, G. Choudhury and S. Dharmaraja, Performance analysis of DRX mechanism using batch arrival vacation queueing system with N-policy in LTE-A networks. Ann. Telecommun. 75 (2020) 353–367. [Google Scholar]
  • C.R. Kalita and G. Choudhury, A note on reliability analysis of an N-policy unreliable 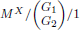Formula queue with optional repeated service. RAIRO-Oper. Res. 52 (2018) 713–724. [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  • C.R. Kalita and G. Choudhury, Analysis of an unreliable 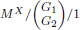Formula repeated service queue with delayed repair under randomized vacation policy. Commun. Stat. Theory Methods 48 (2019) 5336–5369. [CrossRef] [Google Scholar]
  • J.C. Ke, H.I. Huang and Y.K. Chu, Batch arrival queue with N-policy and at most J vacations. Appl. Math. Modell. 34 (2010) 451–466. [Google Scholar]
  • J. Keilson and L.D. Servi, Oscillating random walk models for GI/G/1 vacation system with Bernoulli schedules. J. Appl. Probab. 23 (1986) 790–802. [Google Scholar]
  • R.F. Khalaf, K.C. Madan and C.A. Lucas, An M[X]/G/1 queue with Bernoulli schedule, general vacation times, random breakdowns, general delay times and general repair times. Appl. Math. Sci. 5 (2011) 35–51. [Google Scholar]
  • A. Krishnamoorthy, P.K. Pramoda and T.G. Deepak, On a queue with interruptions and repeat or resumption of service. Nonlinear Anal. 71 (2009) 1673–1683. [Google Scholar]
  • M.S. Kumar and R. Arumuganathan, An MX/G/1 unreliable retrial queue with two phase service and persistence behaviour of cuatomers in service. RAIRO-Oper. Res. 47 (2013) 9–32. [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  • S. Lan and Y. Tang, An N-Policy discrete-time GEO/G/1 queue with modified multiple server vacations and Bernoulli feedback. RAIRO-Oper. Res. 53 (2019) 367–387. [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  • H.S. Lee and M.M. Srinivasan, Control policies for the MX/G/1 queueing system. Manage. Sci. 35 (1989) 708–721. [Google Scholar]
  • H.W. Lee, S.S. Lee and K.C. Chae, Operating characteristic of MX/G/1 queue with N-policy. Queueing Syst. 15 (1994) 387–399. [Google Scholar]
  • Q. Li, D. Xu and J. Cao, Reliability approximation of a Markov queueing system with server breakdown and repair. Microelectron. Reliab. 37 (1997) 1203–1212. [Google Scholar]
  • W. Li, D. Shi and X. Chao, Reliability analysis of M/G/1 queueing systems with server breakdowns and vacations. J. Appl. Probab. 34 (1997) 546–555. [CrossRef] [MathSciNet] [Google Scholar]
  • T. Li, L. Zhang and S. Gao, An M/G/1 retrial queue with single working vacation under Bernoulli. RAIRO-Oper. Res. 54 (2020) 471–488. [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  • K.C. Madan, A queueing system with random failures and delayed repairs. J. Indian Stat. Assoc. 32 (1994) 39–48. [Google Scholar]
  • K.C. Madan, An M/G/1 type queue with time-homogeneous breakdowns and deterministic repair times. Soochow J. Math. 29 (2003) 103–110. [Google Scholar]
  • K.C. Madan, A.D. Al-Nasser and A.Q. Al-Masri, On Formula queue with optional re-service. Appl. Math. Comput. 152 (2004) 71–88. [Google Scholar]
  • K.C. Madan, Z.R. Al-Rawi and A.D. Al-Nasser, On 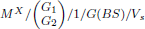Formula vacation queue with two types of general heterogeneous service. J. Appl. Math. Decis. Sci. 3 (2005) 123–135. [Google Scholar]
  • M.K. Maheshwari, A. Roy and N. Saxena, Analytical modeling of DRX with flexible TTI for 5G communications. Trans. Emerging Telecommun. Technol. 29 (2018) e3275. [Google Scholar]
  • F.A. Maraghi, K.C. Madan and K.D. Dowman, Batch arrival queueing system with random breakdowns and Bernoulli schedule server vacations having general vacation time distribution. Int. J. Inf. Manage. Sci. 20 (2009) 55–70. [Google Scholar]
  • J. Medhi, Stochastic Models in Queueing Theory, 2nd edition. Academic Press, Burlington (2003). [Google Scholar]
  • Y. Peng, Z. Liu and J. Wu, An M/G/1 retrial G-queue with preemptive resume priority and collisions subject to the server breakdowns and delayed repairs. J. Appl. Math. Comput. 44 (2014) 187–213. [Google Scholar]
  • H. Saggou, T. Lachemot and M. Ourbih-Tari, Performance measures of M/G/1 retrial queues with recurrent customers, breakdowns, and general delays. Commun. Stat. Theory Methods 46 (2017) 7998–8015. [CrossRef] [Google Scholar]
  • J.F. Shortle, J.M. Thompson, D. Gross and C.M. Harris, General arrival or service patterns. In: Fundamentals of Queueing Theory. Wiley (2018). [CrossRef] [Google Scholar]
  • C.J. Singh, M. Jain and S. Kaur, Performance analysis of bulk arrival queue with balking, optional service, delayed repair and multi-phase repair. Ain Shams Eng. J. 9 (2018) 2067–2077. [Google Scholar]
  • L. Tadj and G. Choudhury, Optimal design and control of queues. TOP 13 (2005) 359–412. [CrossRef] [MathSciNet] [Google Scholar]
  • L. Tadj and J.C. Ke, A hysheretic bulk quoram queue with a choice of service and optional re service. Qual. Technol. Quant. Manage. 5 (2008) 161–178. [Google Scholar]
  • L. Tadj and K.P. Yoon, Binomial schedule for an M/G/1 type queueing system with an Unreliable server under N-policy, Adv. Decis. Sci. 2014 (2014) 819718. [Google Scholar]
  • H. Takagi, Time-dependent analysis of M/G/1 vacation models with exhaustive service. Queueing Syst. 6 (1990) 369–389. [Google Scholar]
  • H. Takagi, Queueing Analysis – A Foundation of Performance Evaluation. Vol 1. Elsevier, Amsterdam (1991). [Google Scholar]
  • H. Takagi, Time-dependent process of M/G/1 vacation models with exhaustive service. J. Appl. Probab. 29 (1992) 418–429. [Google Scholar]
  • N. Tian and Z.G. Zhang, Vacation Queueing Models: Theory and Applications. Springer, New York (2006). [CrossRef] [Google Scholar]
  • J. Wang, An M/G/1 queue with second optional service and server breakdowns. Comput. Math. App. 47 (2004) 1713–1723. [Google Scholar]
  • H. White and L.S. Christie, Queueing with preemptive priorities or with breakdown. Oper. Res. 6 (1958) 79–96. [Google Scholar]
  • R.W. Wolff, Poisson arrivals see time averages. Oper. Res. 30 (1982) 223–231. [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.